【このアイデアを思いついたヒント】 |
発明クラブで正十二面体のことを知り、楽しいと思いました。二個、三個の正十二面体をたこ糸でつるしてたこ糸をねじって回したときの動きがとても不思議に見えたからです。
大小の正十二面体をいくつもたこ糸でつなげて、つり下げて回したら、どんな動きをするのか知りたくなりました。
そこで、たこ糸をつないでつり下げた正十二面体を、同時に三本回して、その動き方の違いを観察できるものを作ろうと考えました。
|
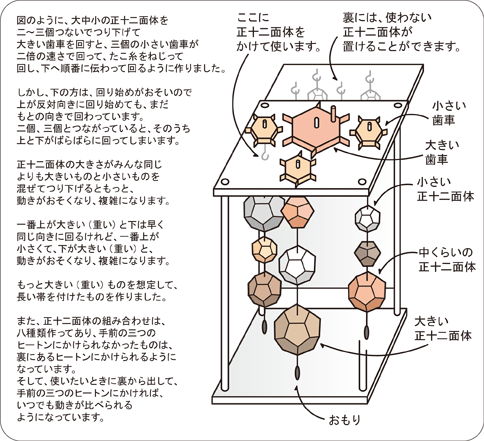
【上の図の説明】 |
| (1) |
大きい歯車を回すと、小さい歯車が二倍の速さで回り、下につり下げたたこ糸をねじります。
たこ糸がねじれると、つり下げた正十二面体がまわります。 |
| (2) |
正十二面体の大きさの違いによって、たこ糸のねじれが正十二面体に伝わる伝わり方が違います。
この違いを観察すると、回転運動の慣性の法則が観察できます。 |
| (3) |
上が大きい正十二面体の下に、小さい正十二面体を付けたときは、小さい正十二面体は上の大きい正十二面体にならって回りますが、上が小さくて下が大きい正十二面体のときには、それぞれの回り方が大変複雑になります。 |
|
【審査委員評】 |
| 大きさの異なる正十二面体三個をたこひもでつないで回転させ、ひものねじれだけでなく、正十二面体の大きさの違いによる慣性力によって回転の伝達が違うことが発見できました。たこひものねじれの力とねじれの方向、そしてその長さ、正十二面体の重さと大きさ、などを変えた時の動きを、詳しく観察して整理してみるともっともっと観察が楽しくなると思います。また、更に発展させて、多面体の面数を変えたり、球面にしたりしても面白いですね。
|